
Wicked Engine
3D engine with modern graphics
Cross-platform technologies





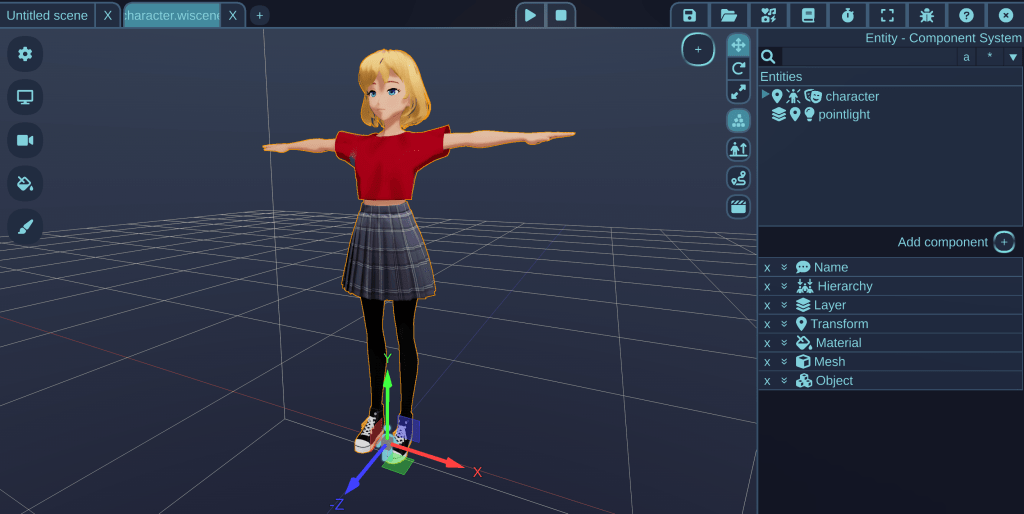
Lightweight editor
Edit models and run scripts with a standalone editor. No internet connection required, no strings attached.
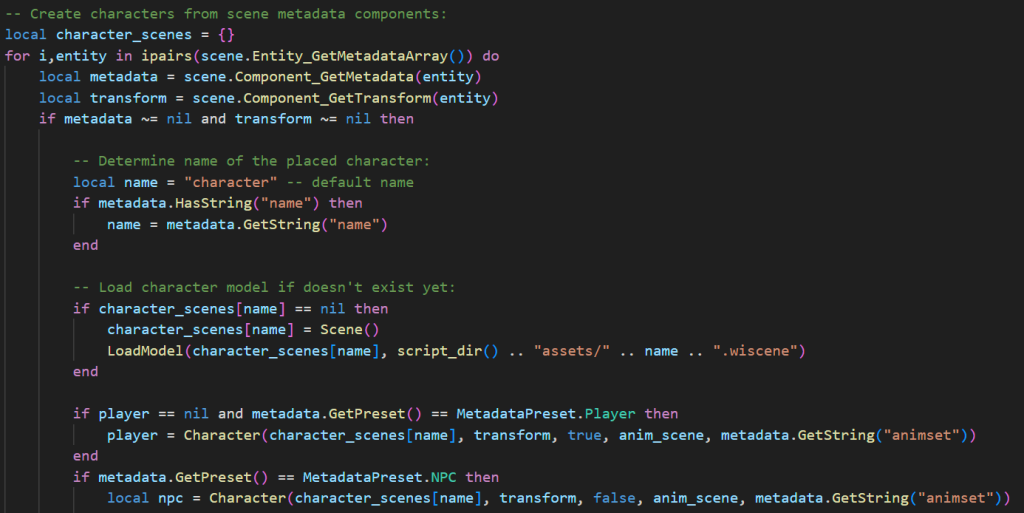
Code-oriented
Enjoy quick and easy Lua scripting, or dive as low level as you want with C++.
VRM characters
Get started with custom characters in your projects quickly and easily!

Realistic rendering
High quality effects, physically based materials, real-time lighting, ray tracing, terrain generation and more…

Pricing
Wicked Engine is free and open source, but you can support the project.
Everyone
Free
You can develop for the Windows, Mac OS and Linux platforms for free.
Supporter 👑
€5.00
Support further development and get exclusive content.
Thank you!
Console developer
TBD
If you are going to release games for consoles, reach out in email.

Join the community
An active developer community to share knowledge with.

Development insights
Take a look at the development blog of Wicked Engine if you are interested in technical details.
You must be logged in to post a comment.